电力电子系统其中包含了大量的电力电子开关,因此具有数不胜数的拓扑数量。求解这样多拓扑数量的电路是非常困难的。但我的工作实现了只用一个迭代矩阵就可以求解系统对应的所有可能拓扑。
相关 文章 已经被发表在 IEEE Transactions on Industrial Electronics。
Background
电力电子系统中的电力电子开关在理想模型下被建模为开和关两种状态。任意一个开关的状态发生变化都会导致系统的拓扑发生变化。面对这样的系统,通常的两种方法都没法很好的解决。
- 方法1: 在求解过程中发生了拓扑变化之后,生成新的方程后用解线性方程的方法进行求解。
- 方法2: 实现求解所有可能拓扑下的离散方程的逆。在拓扑发生变化后,只需要切换成对应的逆矩阵即可。
显然,方法1的计算量是巨大的,而方法2的存储复杂度是随着开关指数上升的。
My Method
- Step 1: Circuit and matrix partitioning 根据switching legs对电路进行划分。Fig. 1,展示了一个经典的DAB电路被划分成了五个部分。其中三个绿色的区域由于不包含任何卡关,因此拓扑是不会发生变化的。利用这样的电路划分来生成状态方程矩阵后,状态方程矩阵结构具有一个特殊的结构——对角矩阵块是不变的,它们对应着电路绿色的部分。非对角块则是对应了包含开关的变化的部分,也就是电路的橙色部分。
- Step 2: Iterative matrix construction 利用这样的特殊的结构,我们如果利用block Jacobi迭代来求解离散后的方程,我们可以推导得到一个恒定的迭代矩阵。所有开关所引起的变化都不会影响这个迭代矩阵。具体过程如Fig. 2所示。(绿色的矩阵块意味着这些数据是不会受到开关的影响的)
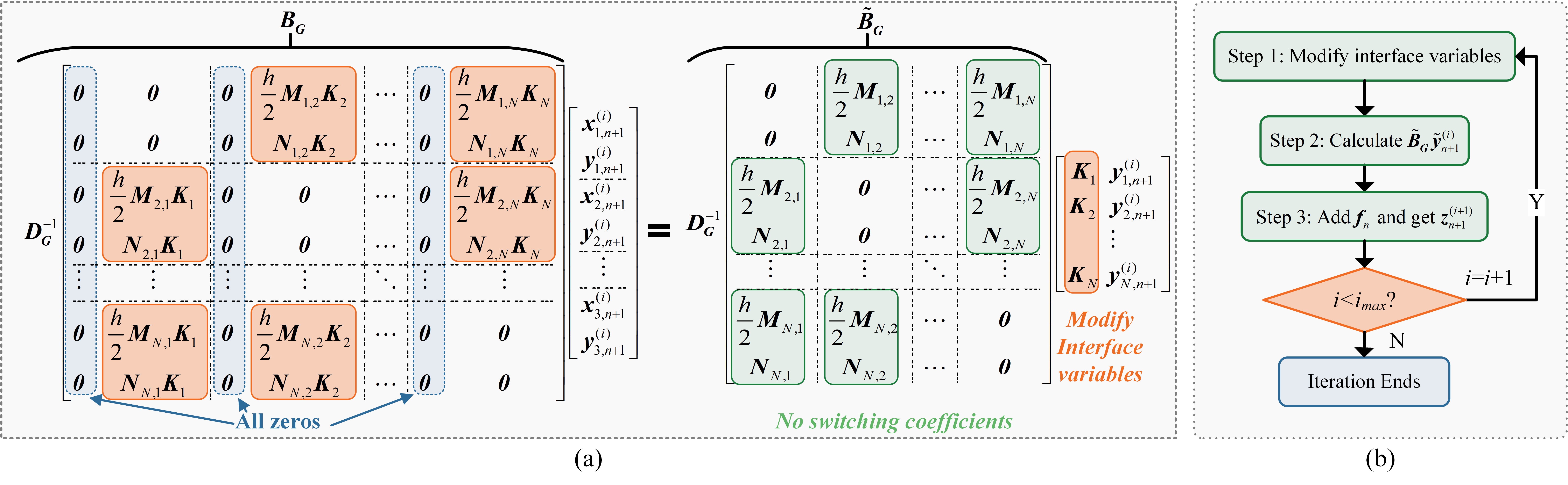
- Conclusion 最终,我们得到了一个恒定的迭代矩阵。不管开关状态怎么变化,我们都只需要利用这一个迭代矩阵进行求解。这样的好处就有三个: 1)节省存储空间:基本只需要存储一个迭代矩阵。 2)规避了迭代法的弊端:通过估算迭代矩阵的谱半径,我们可以提前知道需要几次迭代完成解算。 2)减少计算量:拓扑变化之后,只需要用迭代法就可以实现求解。又由于迭代次数是恒定的(不管什么拓扑之下),因此计算复杂度只有n^2。