Power electronic systems contain numerous power electronic switches, leading to countless possible topologies. Solving circuits with such a large number of topologies is very challenging. However, my work has achieved a method to solve all possible topologies of the system using just one iterative matrix.

The related paper has been publised on IEEE Transactions on Industrial Electronics.

Background

In power electronic systems, power electronic switches are ideally modeled with two states: on and off. Any change in the state of a switch results in a change in the system’s topology. The usual methods to handle such systems often fall short:

• Method 1: After a topology change during the simulation process, generate new equations and solve them using linear equation solving methods.
• Method 2: Pre-compute the inverse of the discrete equations for all possible topologies. When the topology changes, simply switch to the corresponding inverse matrix.

Clearly, Method 1 has a huge computational cost (O($n^3$)), while Method 2 has a storage complexity that increases exponentially with the number of switches.

My Method

• Step 1: Circuit and matrix partitioning

  Partition the circuit according to the switching legs. Fig. 1 shows a classic DAB circuit divided into five parts. The three green regions do not contain any switches, so their topology does not change. Using this circuit partitioning to generate the state equation matrix results in a special structure—the diagonal matrix blocks remain constant, corresponding to the green parts of the circuit. The off-diagonal blocks correspond to the changing parts of the circuit, which are the orange parts.

Fig. 1: Circuit Partitioning

• Step 2: Iterative matrix construction

  Utilizing this special structure, we can derive a constant iterative matrix if we use the block Jacobi method to solve the discretized equations. All the changes caused by the switches do not affect this iterative matrix. The specific process is shown in Fig. 2 (green matrix blocks indicate data that is unaffected by the switches).

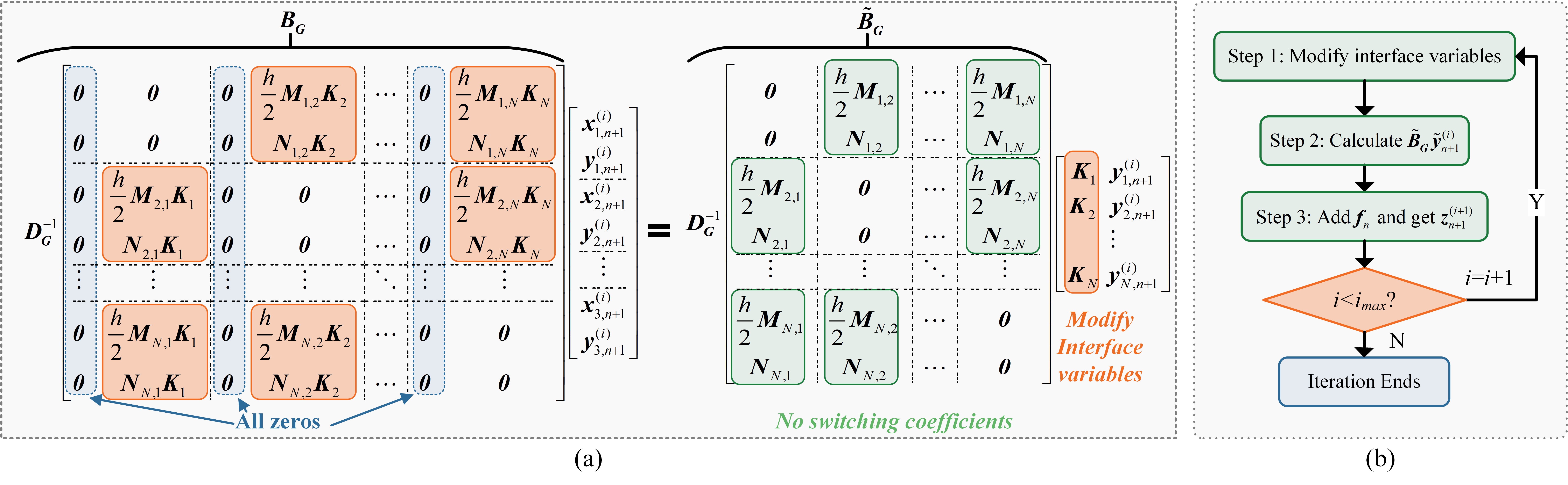
Fig. 2: How to derive the iterative matrix?

• Conclusion

  Finally, we obtain a constant iterative matrix. Regardless of how the switch states change, we only need to use this one iterative matrix for solving. This has three main benefits:

  1. Storage Efficiency: Only one iterative matrix needs to be stored.
  2. Mitigation of Iterative Method Drawbacks: By estimating the spectral radius of the iterative matrix, we can know in advance how many iterations are needed to complete the solution.
  3. Reduced Computational Complexity: After a topology change, the solution can be achieved using the iterative method. Since the number of iterations is constant (regardless of topology), the computational complexity is only O(( n^2 )).